Algorithm
[자료구조와 알고리즘 - 기초#4] 알고리즘 성능 표현, 빅 오 표기법
by Roseline Song | January 17, 2019
알고리즘의 시간을 표현할 때 ‘빅 오 표기법’을 쓴다. 알고리즘 실행에 필요한 단계를 나타내기 위해 컴퓨터 공학자들이 수학에 쓰이는 용어를 가져온 것이다.
수학에서의 ‘빅 오’란?
빅 오는 수학에서는 함수의 성질을 나타낼 때 쓰이는 말이다. 함수 증가율의 상한값으로 설명되기도 한다. 또는 함수 g(x)가 f(x)의 속도보다 빠를 수 없을 때, g는 O(f)에 속한다고 하기도 한다. 예를 들어, g(x) = x이고, f(x) = 2x라고 할 때, g(x)는 f(x)의 값보다 빠를 수(혹은 클 수) 없다. 이때 g는 O(f)에 속한다고 할 수 있다. 어렵다면 겁먹지 말고 일단 다음으로 넘어가자.
※ 상한값 : 집합 Y의 요소 안에서 다른 모든 원소들보다 가장 큰 실수를 상계라 한다. 이때 상계 중 가장 작은 값을 상한값이라고 한다. 예를 들어, 음수인 실수만을 원소로 가지는 집합 X가 있다고 할 때, 집합 X의 상계는 0 또는 양수인 실수이다. 이때 상계 중 가장 작은 값은 0이므로 상한값은 0이다
알고리즘에서의 빅 오
빅 오는 쉽게 생각하면 알고리즘의 실행 단계가 얼만큼되는지 간단하게 표기한 것이라고 할 수 있다. 앞선 포스팅에서 읽기, 검색, 삽입, 삭제 연산을 해봤는데 이번에는 그때 구한 연산 속도를 빅 오로 표기해보자.
읽기 : O(1)
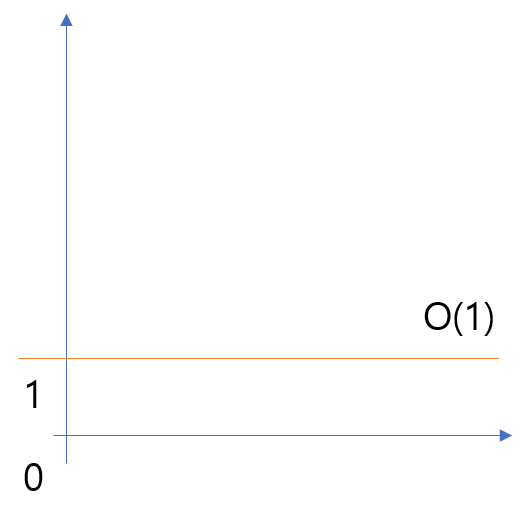
첫 메모리 주소와 인덱스로 원하는 데이터에 한 번에 접근 가능하다. 어느 경우든지 실행 단계는 한 번이기 때문에 O(1)이다. 알고리즘에 필요한 단계가 항상 일정하기 때문에 상수 시간이라고도 한다.
선형 검색 : O(N)
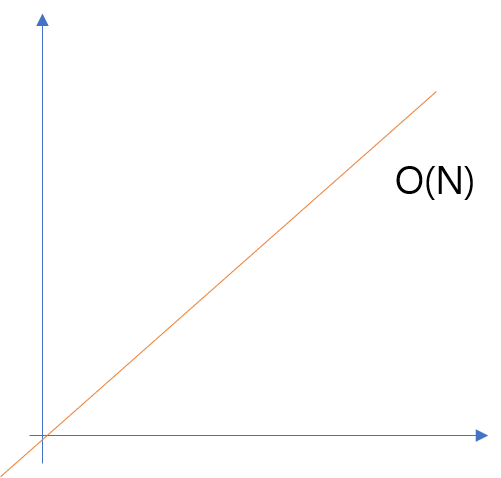
선형 검색의 경우, N개의 요소가 있을 때 N개를 하나하나 다 살펴보아야 한다. 따라서 데이터가 많아질 수록 실행 단계 역시 많아지며, 이 경우’선형 시간’이라고 한다.. 만약, 찾는 데이터가 맨 처음에 위치한다면 한 단계 실행으로 끝날 수 있지만, 빅 오 표기법에서는 최악의 시나리오를 가정해서 최대 몇 단계까지 실행해야 하는지 계산한다.
이진 검색 : O(logN)
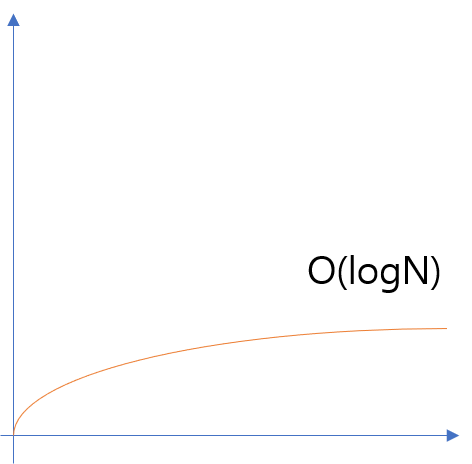
이진 검색은 밑이 2인 상용로그 log2N 단계가 필요하며, 빅 오 표기법으로는 O(log2N)와 같다. 이진 검색이 어떤 과정에서 log2N 단계가 나오는지 보자. 1부터 100까지의 데이터가 있는 정렬 배열이다. 최악의 시나리오로 1또는 100을 찾는다고 가정하는데, 단계 계산을 쉽게 하기 위해 1을 선택한다. 이때 찾고자 하는 값 1을 key라고 부르자.
| 범위 | 질문 | 결과 | 단계 |
|---|---|---|---|
| 1 ~ 100 | key >= 50 ? | False | step 1 |
| 1 ~ 49 | key >= 25 ? | False | step 2 |
| 1 ~ 24 | key >= 13 ? | False | step 3 |
| 1 ~ 12 | key >= 7 ? | False | step 4 |
| 1 ~ 6 | key >= 4 ? | False | step 5 |
| 1 ~ 3 | key >= 2 ? | False | step 6 |
| 1 | key= 1 ? | True | step 7 |
1을 찾을 때까지 배열을 계속 2로 나눈다. 1 ~ 100까지의 수에서 1을 찾으려면 2로 7번 나눠야 하며, 1 ~ 1000까지의 수에서 1을 찾기 위해서는 2로 10번 나눠야한다. 범위에 따라 필요한 실행 단계를 표로 나타내면 아래와 같다.
| 범위 | 단계 |
|---|---|
| 1 ~ 10 | 2로 4번 나눈다. |
| 1 ~ 100 | 2로 7번 나눈다. |
| 1 ~ 1000 | 2로 10번 나눈다. |
| 1 ~ 10000 | 2로 14번 나눈다. |
의 의미는 2를 x 번 거듭제곱하면 N이 나온다는 뜻이다. 예를 들어, 일 때 2를 3번 거듭제곱하면 N이 나온다는 뜻이므로 N은 이다. 즉, N은 8이며 O()이면 실행 단계는 3이다. 따라서, 에서 N은 전체 요소의 개수이고, x는 실행 단계라고 할 수 있다.
만약 우리가 찾는 수가 1000이라 하고, 실행 단계를 다음과 같이 나타내보자.
범위가 1부터 1000일 때, 실행 단계 : (x는 실행 단계이므로 자연수)
512는 이므로
1024는 이므로 이다.
따라서, 은 9.xxxxx 이지만, x는 실행 횟수라 자연수로 세야하므로 올림하여 10번이 된다.
따라서 이진 검색의 실행 단계를 나타내는 빅 오는 O() 로 나타낸다. 보통 로그의 밑인 ‘2’는 생략하고 쓰며, ‘(빅) 오 로그 N’이라고 읽는다. 또한, 이러한 유형의 시간복잡도를 ‘로그 시간’이라고 한다.
Subscribe via RSS