자료구조와 알고리즘을 왜 배우는 걸까? 결론부터 말하면, 같은 연산이라도 자료 구조와 알고리즘에 따라 연산의 단계가 달라지기 때문이다. 알고리즘이 실행 속도에 영향을 준다는 것은 상식적으로 이해 가능하니, 아래 예시에서 자료 구조가 실행 속도에 어떻게 영향을 줄 수 있는지 알아보자.

배열의 연산 : 읽기, 검색, 삽입, 삭제

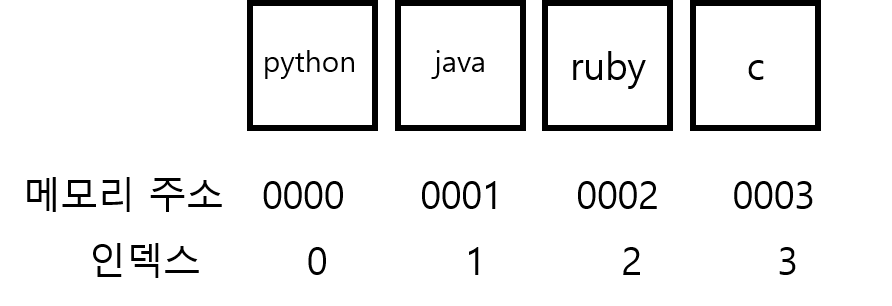
읽기

인덱스와 메모리 주소를 통해 데이터에 접근한다. 컴퓨터는 배열의 첫번째 메모리 주소를 알고 있다. 찾으려고하는 데이터가 인덱스 3에 있다면, 첫번째 메모리 주소에 인덱스를 더해 원하는 데이터의 메모리로 바로 접근한다.

검색

“c”라는 값을 가진 데이터를 배열에서 찾으라고 명령하면, 값이 “c”인 데이터가 나올 때까지 인덱스 0부터 3까지 하나하나 확인한다. 이렇게 컴퓨터가 각 요소를 하나하나 확인하는 것을 ‘선형 검색’이라고 한다.

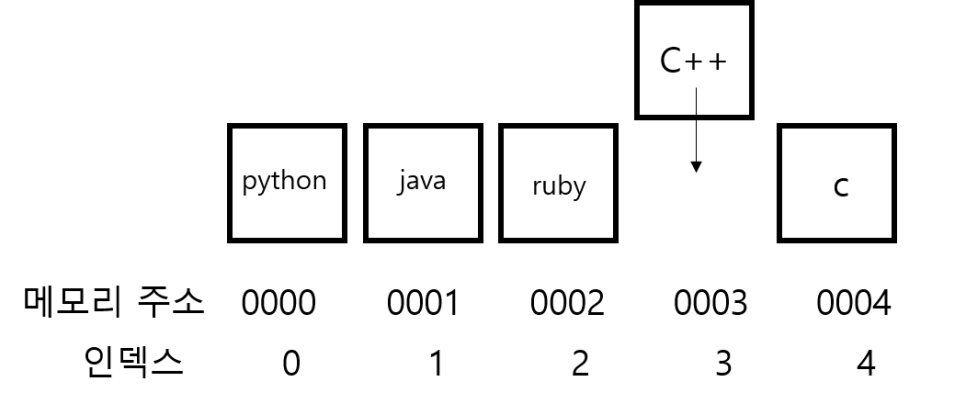삽입

삽입

배열 중간에 데이터를 삽입할 때, 넣을 공간 오른쪽에 있는 셀을 한 칸씩 민다. 그리고 빈 공간에 원하는 데이터를 삽입한다. 위에서는 원래 인덱스 3에 있던 셀을 오른쪽으로 밀고, 빈 공간에 데이터를 넣었다. 만약 인덱스 2에 삽입한다면, 처음에는 c 셀을 밀고, 그 다음에는 ruby셀을 민 다음 비어 있는 인덱스 2 공간에 삽입한다. 최선의 경우는 맨 끝에 삽입하는 것이고, 최악의 경우는 맨 처음에 삽입하여 처음부터 끝까지 다 한 칸씩 밀어내는 것이다.

삭제

데이터를 먼저 삭제하고, 오른쪽에 있는 나머지 데이터를 왼쪽으로 당겨 빈 공간을 채운다. 인덱스 1을 삭제했다면, ruby 셀을 당기고 그 다음 c 셀을 당긴다. 이것도 삽입과 마찬가지로 최선은 맨 끝을 삭제하는 것이고, 최악은 맨 처음을 삭제하는 것이다.

​

각 연산에서 걸리는 단계를 생각해보자. 단계를 계산할 때는 최악의 경우를 가정한다.

• 읽기 : 먼저 읽기의 경우, 배열 요소의 개수와 상관 없이 메모리 주소와 인덱스를 통해 바로 데이터에 접근하므로 실행 횟수는 항상 1번이다.

• 검색 : 셀을 하나씩 검사한다. 내가 원하는 데이터가 배열의 맨 끝에 있다는 최악의 경우를 가정하면, N개의 요소가 있을 때 N단계를 거친다.

• 삽입 : 끝에 삽입하는 경우는 항상 1번 실행한다. 하지만 맨 처음에 삽입하는 최악의 경우, N개의 요소를 N번씩 오른쪽으로 밀고 마지막 1번 삽입하는 과정을 거쳐 N + 1 단계를 거친다.

• 삭제 : N개 요소 중 하나를 삭제했다면, 나머지 N - 1개를 왼쪽으로 당겨야 한다. 최악의 경우는 역시 삽입과 마찬가지로 맨 처음 데이터를 삭제하는 것이다. 만약 그렇다면 삭제 한 단계와, N-1개 요소를 당기는 단계가 필요하므로 총 N단계를 거친다.

집합의 연산

자료 중 집합(set)은 ‘중복을 허용하지 않는다’. 읽기와 검색의 경우, 원래 있는 데이터를 찾는 것이므로 배열과 연산의 단계는 똑같다(삭제 역시 중복과는 관계 없으므로 연산 단계는 배열과 같다). 하지만, 삽입할 때는 새로 넣고자 하는 데이터가 기존 데이터와 중복되지 않는지 ‘검색’해봐야하기 때문에 N개의 요소가 있다면 N번씩 검사해야 한다. 이 과정에서 배열의 삽입 연산에서 걸리던 N + 1 단계에 N 단계가 추가된다. 즉, 집합에서의 삽입은 2N + 1 단계가 걸린다.

이 결과를 통해 알 수 있는 것은 알고리즘뿐만 아니라 자료구조에 따라서도 실행의 속도가 달라질 수 있음을 의미한다. 최선의 프로그램을 만들기 위해서는 연산 속도에 영향을 주는 자료구조와 알고리즘을 배운다.