Algorithm
[자료구조와 알고리즘 - 기초#5] 빅 오 표기법의 특징 3가지
by Roseline Song | January 19, 2019
배열에서의 삽입 연산은 (N+1)단계의 실행이 필요하고, 집합은 새로운 요소가 기존 요소와 중복되는지 검사하기 위해 삽입 연산에 검색 연산까지 더하여 (2N+1)단계의 실행이 필요하다. 실행 단계로만 보면 삽입 연산에서 배열보다 집합의 연산 시간이 2배로 걸린다. 하지만 빅 오 표기법으로 두 연산을 나타내면 똑같이 O(N)으로 나타낸다. 왜 그럴까? 그 이유는 빅 오 표기법이 가진 특징때문이다.
빅 오 표기법 특징 3가지
- 최악의 시나리오를 가정한다.
- 상수를 무시한다.
- 가장 높은 차수만 인정한다.
1. 최악의 시나리오를 가정한다.
항상 최악의 시나리오를 가정하는 것은 아니다. 그러나 최선의 시나리오를 명시하지 않는 이상, 일반적으로 최악의 시나리오로 가정한다. *선형 검색의 경우, 찾고자 하는 데이터가 맨 처음에 있다면 첫번째 단계에서 끝나며 빅 오로는 O(1)로 표기한다. 엄청난 운의 소유자가 아니라면 항상 찾고자 하는 데이터가 맨 처음에 존재하기는 어렵다. 그래서 최악의 시나리오를 가정하여 빅 오 O(N)으로 표기하면, ‘아 최대 이 정도 단계를 거치겠구나’하고 가늠할 수 있다. 최선을 기대하기보다는 최악을 대비하는 것이 더 나은 알고리즘을 짜는데 더 유용하다는 지론이다. (※하지만 항상 그런 것은 아니다. 뒤에 나오겠지만, 최악보다는 평균적인 시나리오를 고려하는 게 더 나을 수 있다.)
*선형 검색 : 데이터 맨 처음부터 끝까지 하나하나 검사하는 연산
2. 상수를 무시한다.
맨 처음에 얘기했던 내용이다. 배열의 삽입 연산은 N + 1단계이고, 집합의 삽입 연산은 2N + 1단계인데 빅 오 표기법은 왜 똑같이 O(N)일까? 같은 알고리즘에서는 분명히 2N + 1의 연산이 더 오래 걸린다. 하지만 다른 연산과 삽입 연산을 비교하는 등 다른 분야의 알고리즘끼리 비교한다면, N + 1단계나 2N + 1단계를 구분하는 것이 무의미해진다. 그래서 상수를 무시하는 것이다. 이해가 안갈테니 예시를 보자.
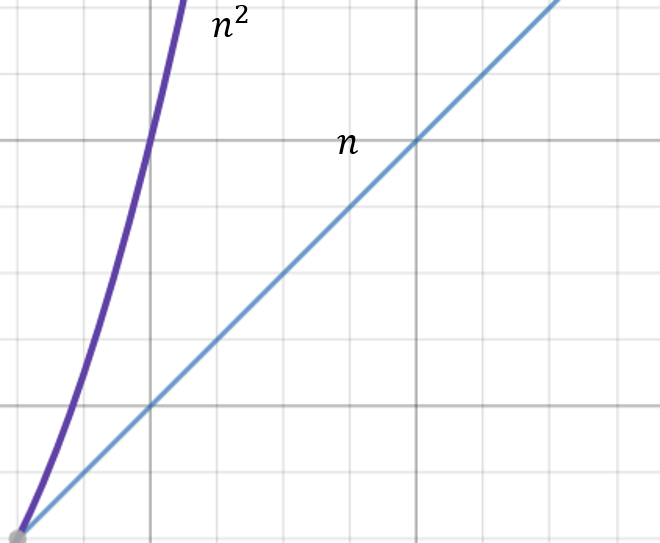
데이터 원소의 개수는 항상 1 이상이므로, 은 항상 맞다. 즉 이 보다 항상 빠르다.
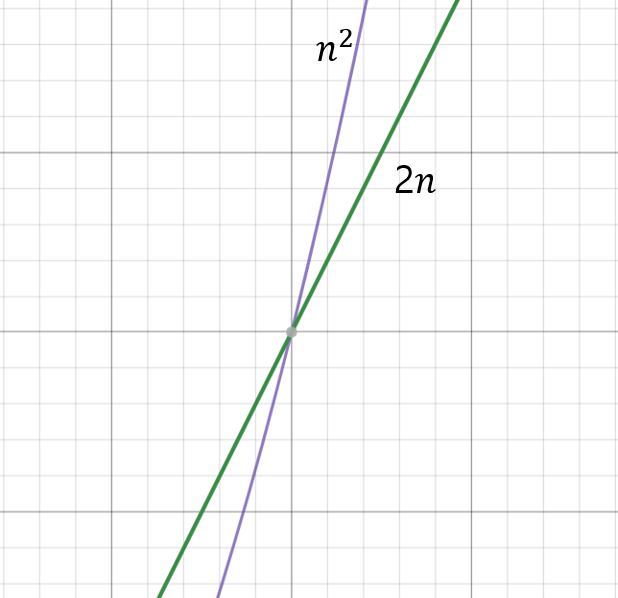
은 처음에는 보다 속도가 느리지만, 특정 원소 개수를 초과하는 순간부터 의 속도보다 빨라진다. 원소 개수가 많아지는 특정 시점부터는 이나 이나 보다 빠른 건 확실하다. 따라서 빅 오 표기법에서는 이나 을 상수로 구분하는 것이 의미가 없는 것이다. 이는 다른 알고리즘끼리 비교할 때는 아주 유용하다. 훨씬 단순하게 연산 속도를 비교할 수 있으니까. 그러나 같은 알고리즘 안에서 연산 속도를 비교하려면, 이나 과 같은 상수의 차이도 감안해야 한다.
3. 가장 높은 차수만 인정한다.
분명 다른 차수의 실행 단계도 연산 속도에 영향을 미칠텐데, 왜 가장 높은 차수만 인정하는 것일까? N의 값, 즉 데이터 원소의 갯수가 엄청나게 많다고 상상해보면, 나머지 차수의 값들은 연산 속도에 큰 영향을 미치지 않기 때문이다.
| 2 | 4 | 8 | 16 |
| 5 | 25 | 125 | 625 |
| 10 | 100 | 1000 | 10000 |
| 1000 | 1,000,000 | 1,000,000,000 | 1,000,000,000,000 |
에 비하면 값은 근소한 차이일 뿐이다. 따라서 빅 오에서는 이나 에 큰 차이가 없기에 연산 속도에 가장 큰 영향을 주는 가장 큰 차수만 인정한다.
Subscribe via RSS