가중합

입력값과 가중치를 곱하고, 바이어스를 더한 값을 말한다. 가중치를 계산해 합한 값이라고 생각하면 쉬울 것 같다.

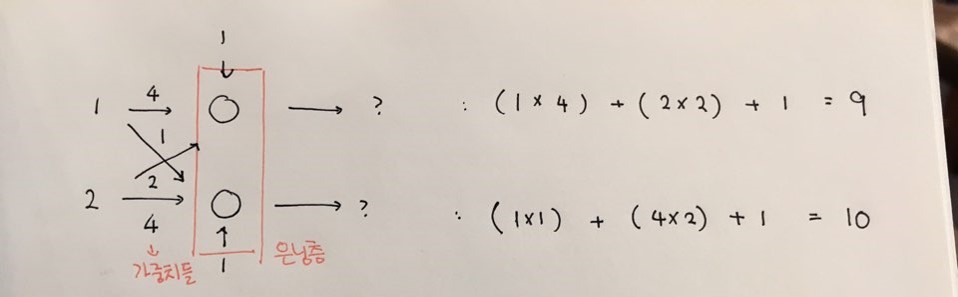
입력층

사진에서 입력값들은 1과 2다.

은닉층

입력층과 출력층 사이에는 은닉층이 존재한다. 은닉층 첫번째 노드는 입력 노드 1로부터 가중치 4, 입력 노드 2로부터 가중치 2를 갖는다. 그리고 1이라는 바이어스 값을 갖는다.

은닉층 두번째 노드는 입력 노드 1로부터 가중치 1, 입력 노드 2로부터 가중치 4를 갖는다. 그리고 1이라는 바이어스 값을 갖는다.

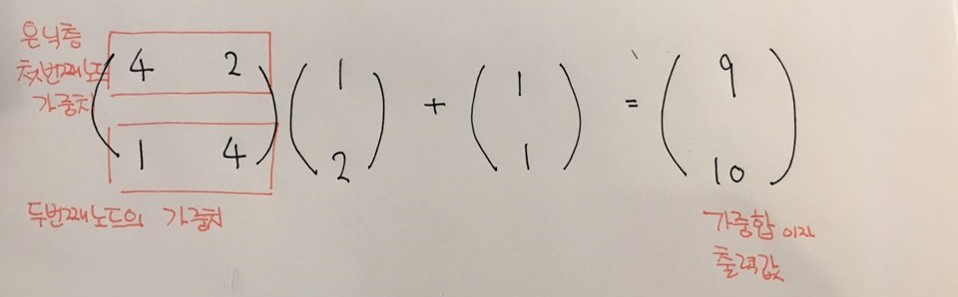
은닉층에서는 각 입력값과 가중치를 곱하고 바이어스를 더해 가중합 9와 10을 출력한다. 위의 계산 과정을 행렬로 나타내면 Wx + b = V와 같다.

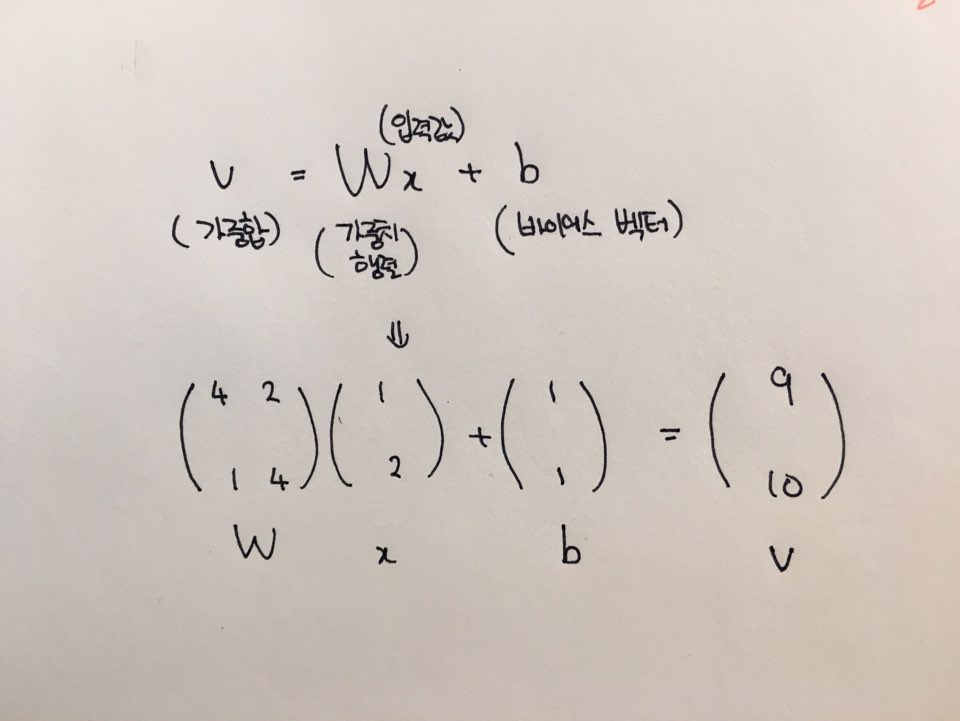
W는 가중치들을 모아놓은 가중치 행렬이다. 첫번째 행은 은닉층의 첫번째 노드가 갖는 가중치, 두번째 행은 은닉층 두번째 노드가 갖는 가중치가 위치한다. 이 가중치 행렬에 곱하는 것은 입력층 x이다. 그리고 바이어스 벡터 b를 더한다. 이렇게 계산하여 나온 벡터를 가중합 v라고 한다. (선형 함수를 썼기 때문에 가중합이 그대로 출력된다.)

※ 벡터 : (N, 1) 형태의 행렬을 벡터라고 부른다.

활성화 함수로 비선형 함수를 쓰는 이유

활성화 함수로 비선형 함수를 쓰면 다층 신경망을 구성하는 이유가 없다. 아래 사진에서 왼쪽 신경망은 여러 은닉층으로 구성되어있지만, 결국 행렬 값을 계산해보면 오른쪽의 단층 신경망과 같은 값이 나온다. 즉, 단층 신경망을 구성해도 같은 값이 나온다면 복잡하게 다층 신경망을 구성할 이유가 없다는 것이다.

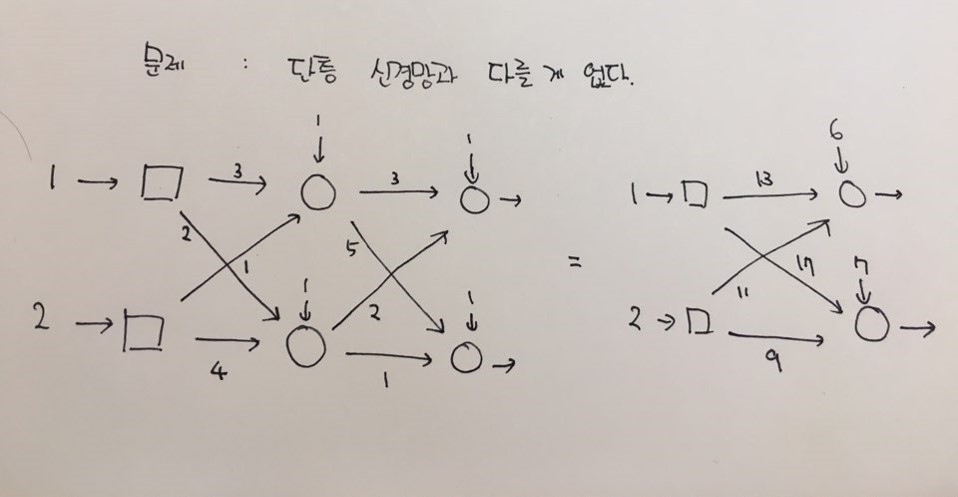
※ 환공포증 주의

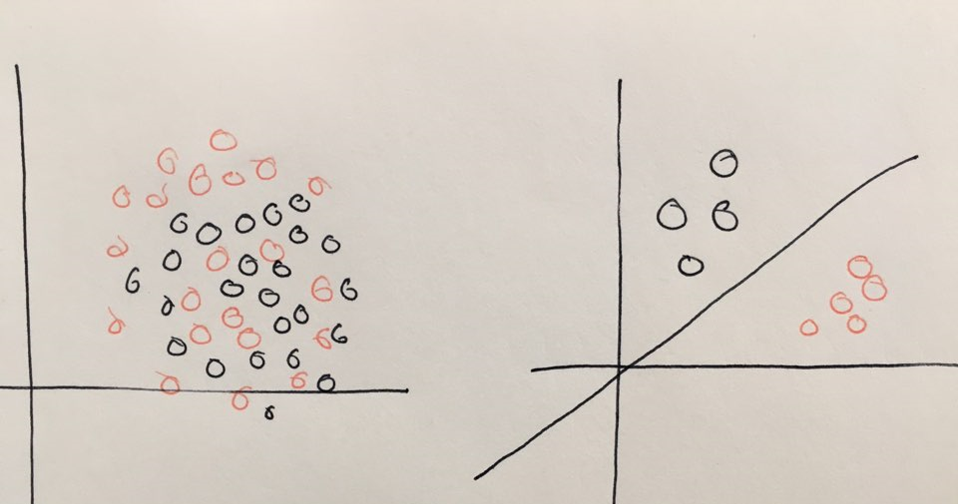
하지만 선형 함수를 사용하면 아래 사진의 오른쪽 그림처럼 선형 분리 문제만 해결할 수 있다. 무당벌레랑 나비를 구분한다고 했을 때 오른쪽처럼 특징이 깔끔하게 갈리면 선형 함수로 해결할 수 있다. 하지만 왼쪽 그림처럼 나선형이나 곡선 등 비선형 함수로 풀 수 있는 문제는 선형 함수로 풀 수 없다. 따라서 활성화 함수로 ‘비선형 함수’를 사용하는 것이다. 단 출력노드에서는 선형 함수를 써도 된다. (회귀 문제의 경우 마지막 출력 노드에서 선형 함수를 쓰기도 한다.)