단층 신경망 학습 규칙

학습 규칙은 가중치를 체계적으로 변경하는 방법을 말한다. 델타 규칙은 단층 신경망의 대표적인 학습 규칙이다.

델타 규칙

학습 데이터를 한 번 훈련해서 답을 구했다. 이를 정답과 비교해보니 ‘오차’가 있었다. 우리가 구한 답이 ‘정답’과 가까워지려면 오차를 줄여야 한다. 입력값이 정해져있으니 입력값에 영향을 주는 ‘가중치’를 갱신해야 한다.

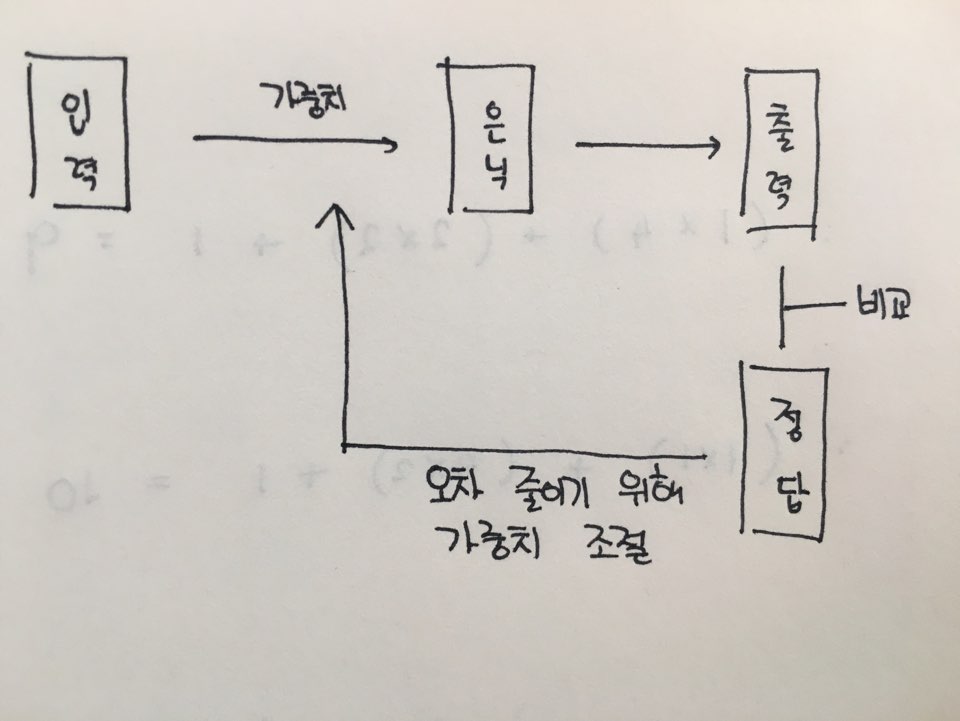
그렇다면 이 가중치는 어떻게 조절할까? 델타 규칙을 써보자. 델타 규칙은 다음과 같다.

어떤 입력 노드가 출력 노드의 오차에 기여했다면, 두 노드의 연결 가중치는 해당 입력 노드의 출력과 출력 노드의 오차에 비례해 조절한다.

좀 더 쉽게 말하면 ‘가중치는 입력노드의 출력(x)과 오차(e)에 비례해 조절‘한다. 수식으로 표현하면 다음과 같다.

w <- w + αex

※ 팁 : 그리스문자를 쓰려면 ㅎ + 한자, 수학 기호는 ㄷ + 한자

여기서 α는 학습률(0 < α ≤ 1)에 해당한다. 학습률은 가중치를 얼마나 바꿀지 조절하는 역할을 한다. 너무 크게 잡으면 정답 근처에서만 왔다갔다하면서 수렴하지 못하고, 너무 작으면 정답에 접근하는 속도가 매우 느려진다. 왼쪽의 가중치는 오른쪽의 식을 계산해 나오는 ‘갱신된 가중치 값’이다.

위의 식에서 αex는 기존 가중치 w에 더해 새로운 가중치를 만든다. 여기서는 Δw라고 하자. 수식으로 다시 표현하면 아래와 같다.

w <- w + Δw

반복 학습

델타 규칙은 반복해서 학습시키며 정답에 근접해 간다. 학습률을 너무 크게도, 너무 작게 잡지도 않으며 가중치를 조절한다. 학습을 반복하면서 오차를 줄이고 정답에 조금씩 근접해 간다.

반복해서 학습시키는 이유는 이렇게 과정을 반복하며 정답을 찾아가는 알고리즘이기 때문이다. 델타 규칙은 ‘경사하강법(Gradient Descent)’라는 수치 해석 기법의 일종이다. 경사하강법은 임의의 초기값에서 시작해 단계적으로 정답을 찾아나간다.

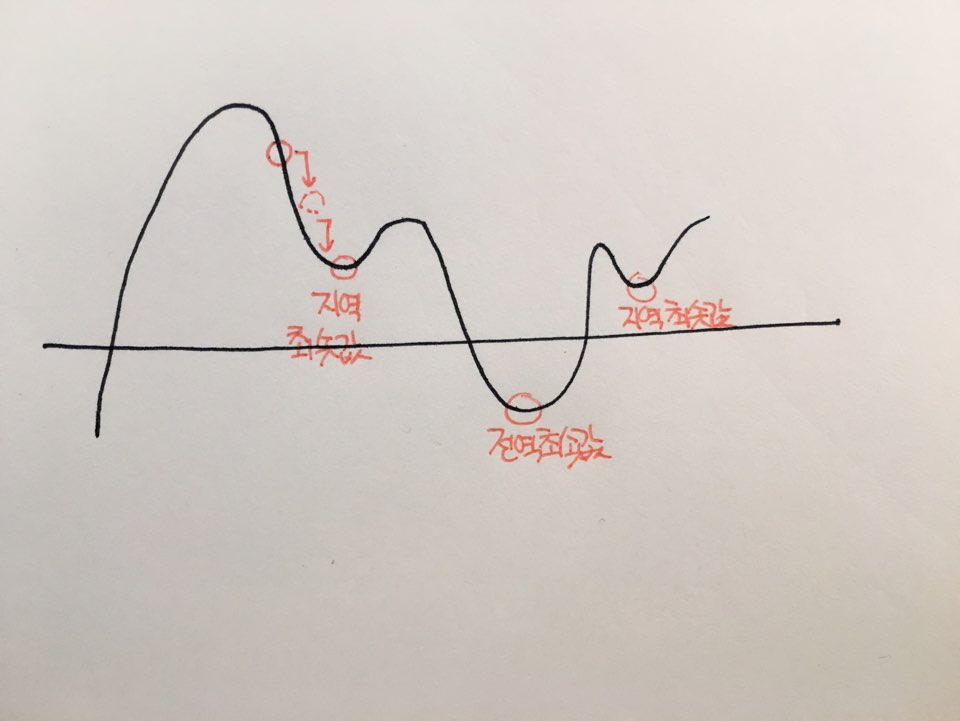
경사하강법은 산에서 공을 굴리면 경사가 가장 급한 길을 따라 가장 낮은 곳까지 굴러가는 것과 비슷하게 정답을 찾아간다고 해서 붙인 이름이다.

산에서 중간중간에 위치하는 낮은 곳은 경사하강법에서 ‘지역 최소값’, 산에서 가장 낮은 곳은 ‘전역 최소값’이라고 한다. 학습을 통해 나온 ‘답’은 이렇게 중간중간 위치하는 낮은 곳들을 찾은 것이고, 그중 가장 낮은 위치의 ‘답’을 정답과 비교한다.

활성 함수에 대한 델타 규칙

앞에서 소개한 델타 규칙은 옛 버전이고, 좀 더 일반적인 형태의 델타 규칙이 있다.

w <- w + αδx

초기 형태에서 e가 δ로 바뀌었을 뿐이다. 그럼 δ는 뭘까? δ는 다음과 같다. e는 오차, v는 가중합. φ는 활성함수이며 φ’는 이것의 ‘도함수’를 말한다. (도함수란 어떤 함수를 미분하여 얻은 함수이다.) 예를 들어, 활성 함수가 시그모이드 함수라고 하면, 시그모이드 함수의 도함수에 가중합을 넣은 후, 여기에 오차값을 곱하면 δ(델타)가 나온다. 여기서 끝나지 않고 델타 값을 아까 가중치 갱신 식 w <- w + αδx에 넣어줘야 한다.

δ <- φ'(v) * e