Data-analytics
[통계학#9] 카이스퀘어 검정(Chi-Square Test)
by Roseline Song | April 9, 2019
※ 전공 데이터 애널리틱스 강의를 듣고 정리한 내용입니다.
카이스퀘어 검정
모집단의 변량을 추정할 때 쓴다.
카이스퀘어 분포
모집단의 변량을 추정하기 위해 쓰는 분포이다. 카이스퀘어 분포는 일반적으로 다음과 같은 특징을 보인다.
- y-scewed (y축에 편향된) 분포이다.
- square 즉, 제곱이므로 음수가 없다.
- 자유도가 증가할 수록 정규분포에 수렴한다.
1번과 3번은 사진을 보면 이해가 더 쉬울 것이다.
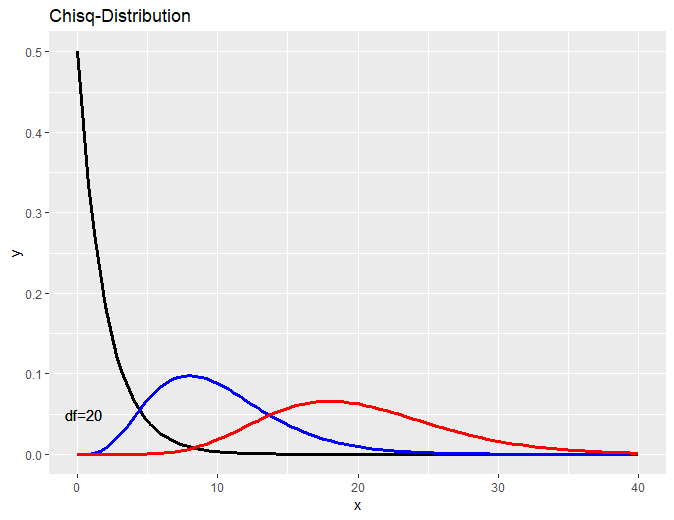 카이스퀘어 분포
카이스퀘어 분포
검정색 선은 자유도(df, degree of freedom)가 2일 때, 파란색 선은 df=10, 빨간선은 df=20일 때이다.
※자유도
자유도는 의 (기울기)처럼 그래프의 형태에 영향을 미치는 수치이다.
카이제곱 분포표
확률 P에 해당하는 가로축의 눈금 의 수치를 기록한 표이다. 아래 사진에서 회색으로 칠해진 부분이 확률 P에 해당한다면 2는 여기에 대응하는 카이제곱 값에 해당한다.
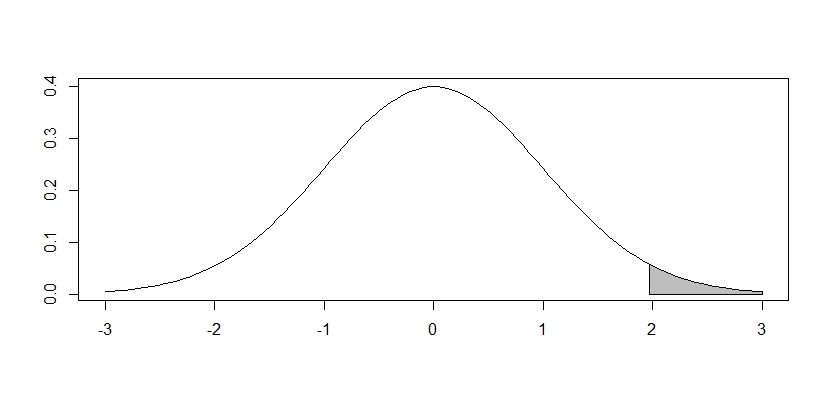
분포표 보는 법
row는 자유도에 해당하고, column은 P 값에 해당한다. df와 p에 해당하는 카이스퀘어값과 실제로 구한 카이스퀘어 값을 비교해서, 실제 카이스퀘어 값이 분포표 값보다 더 크면 귀무가설(Null 가설)을 기각한다.
카이스퀘어 검정 종류 2가지
- goodness of fit (단일 변인의 경우)
- contingency table analysis
goodness of fit은 두 데이터의 모델을 비교할 때 사용한다. 즉, 내가 추정한 데이터의 모델과 모집단의 모델이 비슷한지 확인할 때 쓴다.
예를 들어, 동전을 던지는 100번 던지는 시행을 한다고 할 때 앞면이 나오는 빈도를 카운트한다. 이때, 우리가 기대하는 빈도(기대 빈도)는 50번이다. 실제 던졌을 때 앞면이 나온 횟수가 30번 이라면, 이 30번은 관찰 빈도가 된다.
카이스퀘어 test
는 관찰 빈도, 는 기대 빈도이다. 기대 빈도가 매우 커지면 카이스퀘어 값은 작아진다. 이 작아질 수록, 관찰 빈도와 기대 빈도 사이의 차이가 거의 없다는 의미이다. 따라서 둘의 차이는 적을 수록 좋다.
goodness of fit 예제
맥주 브랜드와 구매량을 보자. 표본 100개 중, 맥주 4개 브랜드가 있다. 기대빈도는 각각 25가 되며(기대빈도에 대한 특별한 언급이 없는 이상), 자유도는 cell - 1이 된다. 이때 주의할 것, 카이제곱에서 자유도는 표본의 크기에서 1을 빼는 게 아니라 cell의 개수에서 1을 빼는 것이다. cell은 변인에 속하는 범주들의 개수라고 생각하면 된다. 맥주 브랜드라는 변인에 4개의 브랜드가 있으니 4-1, 즉 자유도는 3이다.
contingency table 예제
자존감이 일의 성취도에 영향을 미친다는 것을 알아본다.
| 성취도 \ 자존감 | high | medium | low | total |
|---|---|---|---|---|
| high | 17 | 52 | 11 | 60 |
| low | 13 | 43 | 34 | 90 |
| total | 30 | 75 | 45 | 150 |
지금 total 데이터를 제외하면, row의 cell은 2개이고, column 쪽의 cell은 3개이다. 이런 경우, 자유도는 이다. 위의 예시에서는 (3-1)*(2-1) = 2이다.
자존감이 높은 사람이 높은 성취도를 쌓는 비율이 전체 중 얼마를 차지하는 지 어떻게 알 수 있을까? 한 쌍의 행, 열의 total값을 서로 곱한 후, 총 total 150으로 나눈다. 열의 total = 60, 행의 total = 30 이므로 %이다.
여기서 카이스퀘어 값을 구하려면 각 cell의 값을 로 구하고, 각 cell의 모든 값을 합한다. 그리고 위에서 말한 것처럼 관찰 빈도와 기대 빈도의 차이가 적을 수록 귀무가설이 기각될 확률이 높아진다.
Subscribe via RSS