※ K-Mooc 통계학 강의를 듣고 정리한 내용입니다.

표집 분포(Sampling Distribution)

교수님께서는 표본 분포라고 하셨는데, Sampling Distribution을 표집 분포, 표본 분포 혼용해서 쓰는 것 같다. 위키피디아에서는 표집 분포와 표본 분포는 다르다고 설명하고 있다. 그래서 일단 여기서는 ‘표집 분포’라고 쓰겠다.


모집단(Parameter)

모집단의 특성들 μ, σ, P, … 등은 ‘알 수 없는’ 상수이다. 이 특성들은 표본을 통해 ‘추정’, ‘추론’해야 한다.


통계량

모수 추정을 위해 표본을 이용해 만든 함수이다. IQR 역시 모수 추정을 위해 만든 통계량의 일종이다.


임의 표본(Random Sample)

  • 기댓값 E(barX) = μ : 표본이 갖는 기대값은 모평균과 일치
  • 분산 =
  • 표준오차 =




중심 극한 정리(Central Limit Theorem)

모집단이 정규 분포라면, 임의 표본은 bar X ~ N(μ, σ^2 / n)으로 역시 정규 분포가 된다. 또한, 표본의 크기 n이 커질 수록 정규 분포를 띠는 경향이 강해진다(중심 극한 정리, Central Limit Theorem).

임의 표본을 표준화해보자.

※ Z score : Z-test에서 쓰이는 검정 점수


일반적으로 중심 극한 정리는 표본의 크기가 25보다 크면 이용 가능하다.


# Central limit theorem
# floor : 버림
# runifrom : r unifrom 난수, 균일 분포 생성 

x = floor(runif(2500, 0, 10))
x

hist(x)
mean(x)
sd(x)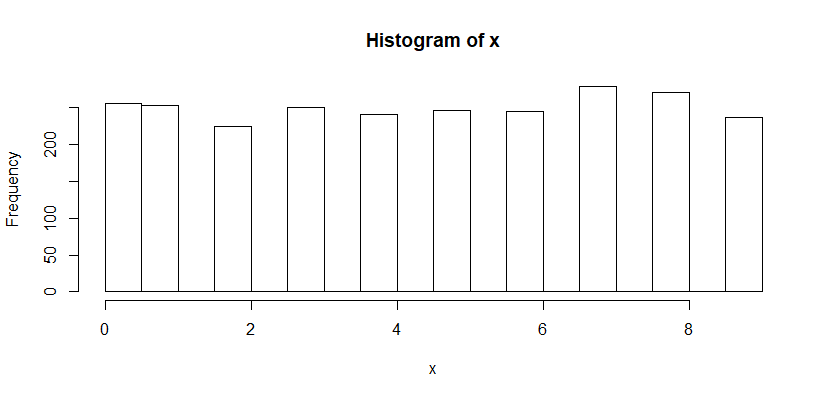


균일 분포

균일 분포의 그래프이다. 샘플링해서 각각의 표본 평균을 구하고, 그래프를 그려보자. 중심 극한 정리대로 샘플의 크기가 충분히 클 때, 정규 분포의 형태를 띠는지 확인한다.


y = array(x, c(500,5))
y # 2500개의 정수를 5개씩 묶어서 500개의 표본으로 만든다.


# 크기가 5인 표본에서 표본평균을 구해 500개의 표본평균 생성
xbar = apply(y, 1, mean) # mean은 위 코드의 균일 분포에서 구한 모평균
xbar

hist(xbar)
mean(xbar)
sd(xbar)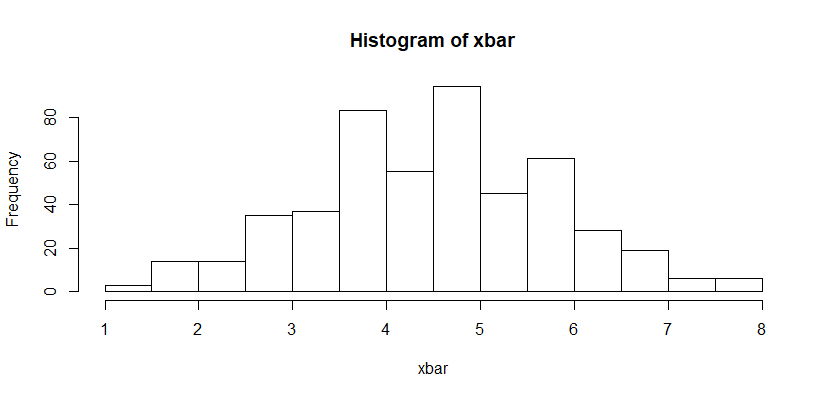


정규 분포의 형태를 띤다