※ K-Mooc 통계학 강의를 듣고 정리한 내용입니다.

정규 분포 (Normal Distribution)

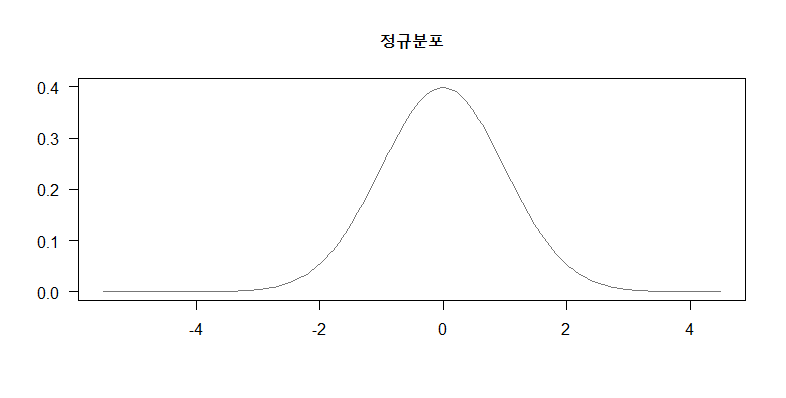
X ~ N(μ, σ^2) (평균, 분산)

• μ에 대해 대칭인 형태를 띤다.
• 확률 변수 X가 μ - 3σ ≤ X ≤ μ + 3σ의 범위 내에 있을 확률은 99.9%이다.
• 분산이 작을 수록 그래프의 폭은 좁아지고 μ에 수렴한다.

아래 그래프를 보면, 빨간색 정규분포의 분산은 1이며, 약간 펑퍼짐한 형태를 띤다. 반면, 파란색 정규분포의 분산은 0.2이며 μ에 수렴하여 뾰족한 형태의 그래프를 그린다. 분산이 커질 수록 그래프는 flat(평평한) 형태에 가까워지며, 분산이 작을 수록 μ에 수렴하여 뾰족한 형태에 가까워진다.

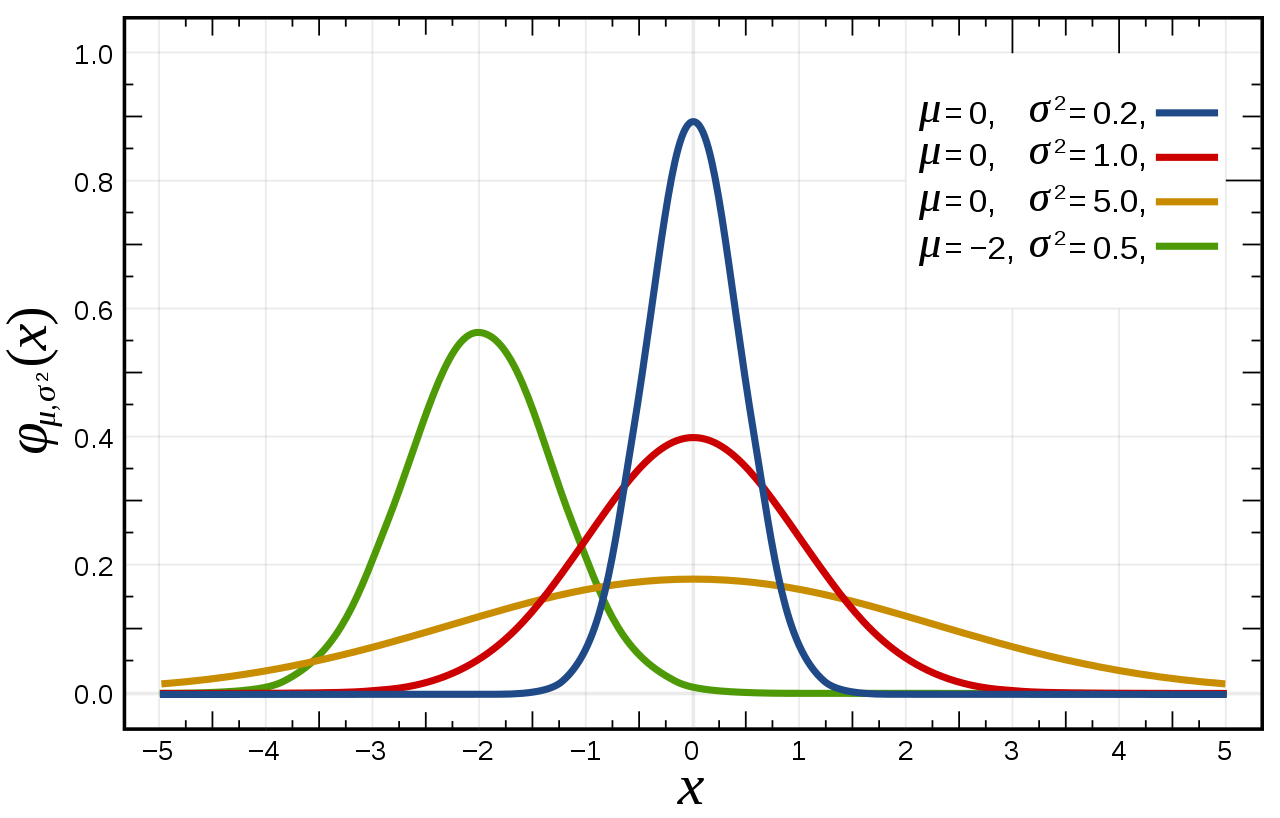출처 : 위키피디아

표준 정규 분포

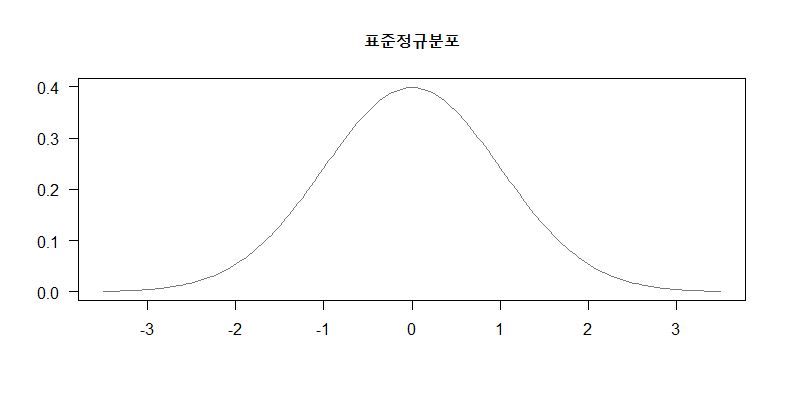
표준 정규 분포는 N(0, 1), 즉 평균 0, 분산은 1인 분포를 말한다.

α = P(Z > z_α)

잠시 후, qnorm(정규 분포의 quantile, 사분위수)에서 나올 α를 설명하면, α는 Z가 z_α보다 클 확률을 말한다.

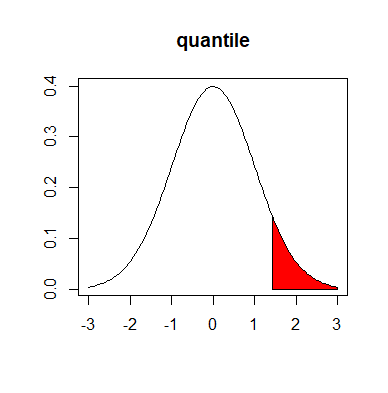
예를 들어, P(Z) > 1.37)에서 Z가 1.37보다 클 확률은 아래 그래프에서 빨간색 면적의 크기에 해당한다. 그 크기는 0.0853이며 α의 값이 된다.

정규분포표 이용 : pnorm, qnorm

1. pnorm(x, μ, σ)

pnorm은 정규분포의 확률을 말한다. pnorm(x, μ, σ)은 N(μ, σ^2)일 때, P(Z ≤ x)일 확률이다.

예를 들어 pnorm(2, 0, 1)은 N(0, 1)이고, 이 정규분포에서 P(Z ≤ 2)일 확률은 0.9772499이다.

# R

pnorm(2,0,1)

2. qnorm(α, μ, σ)

qnorm은 정규분포에서 P(X ≤ x) 를 만족하는 x를 α로 놓는다.

예를 들어, 표준정규분포 N(0, 1)에서 x값 이하의 면적(확률)이 0.03이 되는 x값(α)을 찾으면 -1.880794이 나온다.

# R

qnorm(0.03, 0, 1)

표준화

이항 분포든, 정규 분포든, 모든 분포를 정규 분포의 형태로 만들 수 있다. 이것을 표준화라고 한다. 표준화된 확률 변수는 항상 평균은 0이며, 분산은 1이 된다.

단, 표준화를 할 때, 주의해야 할 2가지가 있다.

• 집단의 크기가 20 이상이어야 하며
• 각 집단은 ‘동질적’이어야 한다.

각 집단이 ‘동질적’이어야 한다는 의미는 뭘까? 예를 들어 학생들이 전국 모의고사를 봤을 때 각 집단의 학업성취도가 ‘유사하다’는 전제를 필요로 한다. 대학생들이 모의고사를 본 점수와 고등학생들이 모의고사를 본 점수를 표준화하려고 하면 이상치(outlier)가 높아져 이상적인 표준정규분포의 형태를 이루기 어렵다. 즉, 표준화를 하려면 각 집단이 어느 정도 동일한 베이스를 이루고 있어야 한다.